Molecular Mass Dataset

# Call Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Here we will take a first look at the molecular mass dataset, taken from Goossens.

#df=pd.read_csv('./c694/goossens_raw.csv')
df=pd.read_csv('./goossens_raw.csv')
df

	SG	TBP(K)	MW
0	0.6310	306	76
1	0.7135	372	99
2	0.7205	365	96
3	0.7293	373	100
4	0.6786	329	82
...	...	...	...
65	0.7054	367	95
66	0.6315	309	72
67	0.8842	353	78
68	1.1762	612	178
69	1.3793	798	300

70 rows × 3 columns

We have 3 variables:

Variable	Description	Designation
\(Mw\)	Molecular Mass	dependent
\(SG\)	Specific Gravity	independent
\(TBP\)	True Boiling Point	independent

We can designate any one of the three as dependent, but as the molecular mass is the most difficult to measure, we’ll chose it.

df.plot(kind='scatter',x='SG',y='MW')
plt.title("Molecular Mass vs Specific Gravity")
plt.grid()
plt.show()

Although there appears to be a clear linear relationship between molecular mass and specific gravity at low gravity numbers, the heteroscedasticity explodes above a gravity of about 0.75.

df.plot(kind='scatter',x='TBP(K)',y='MW')
plt.title("Molecular Mass vs True Boiling Point")
plt.grid()
plt.show()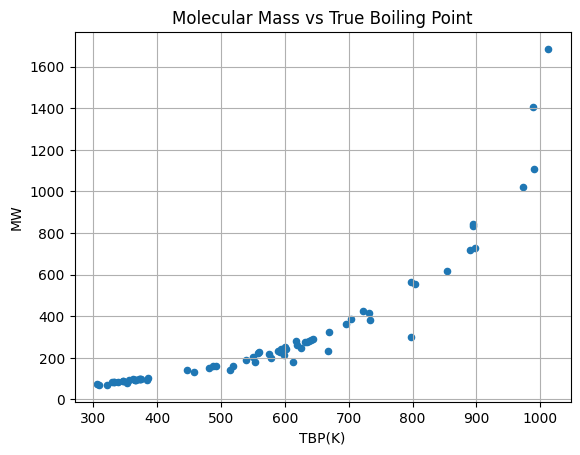

There seems to be a monotonically increasing relationship between molecular mass and true boiling point, with a possible “pole” around the boiling point of 1000.

At this point, it may be tempting to ignore the effect of specific gravity on the prediction of molecular mass.

df.plot(kind='scatter',x='TBP(K)',y='SG')
plt.title("Specific Gravity vs True Boiling Point")
plt.grid()
plt.show()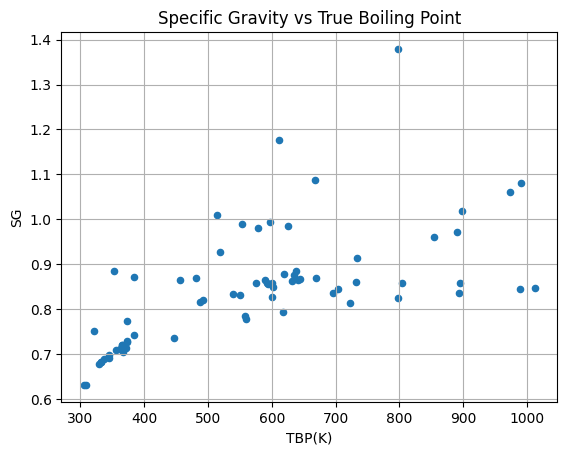

This plot suggests that there is very little correlation between specific gravity and true boiling point, except maybe at low values of boiling point. Lets test this:

c_sg_tbp=np.corrcoef(df['SG'],df['TBP(K)'])
print(c_sg_tbp)

[[1.         0.62521831]
 [0.62521831 1.        ]]